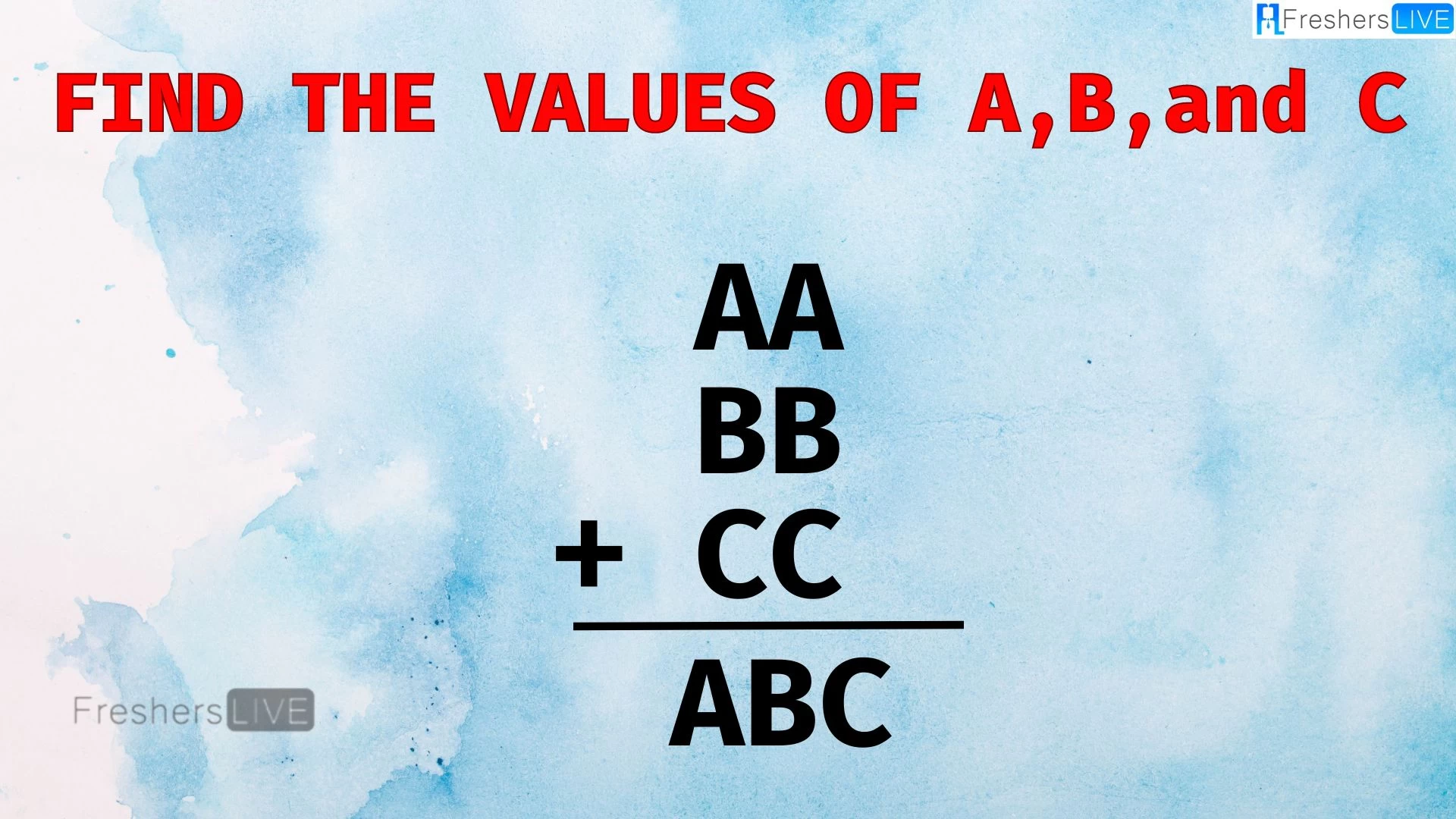It’s fun to solve puzzles that make you think in different ways. If you like solving tricky puzzles and solving them, you should definitely try these. Solving these puzzles can also help reduce stress and fatigue. Check out the puzzle below.
- Observation Visual Test: If you have Hawk Eyes Find the Number 478 among 470 in 13 Secs
- Brain Teaser Math Test: Equate 920÷20×3+6
- Brain Teaser Solve This Amazing Viral Math Puzzle In Less Than 1 Minute
- Test Visual Acuity: If you have Eagle Eyes Find the Inverted 4 in 15 Secs
- Brain Teaser Viral Math Problem 6/2(1+2)=? Solve this Twitter Viral Math Puzzle
What values do A, B, and C represent in the equation AA + BB + CC = ABC?
Math puzzles allow you to use your problem-solving skills. They are designed to make you think carefully, analyze the information you have, and use mathematics to find answers.
You are watching: What Values Do A, B, and C Represent in the Equation AA + BB + CC = ABC?

The image above shows a puzzle, and to solve it you need to find the hidden patterns that control its various parts. But there’s a challenge: You have to spot patterns quickly. You need to think quickly and be good at analyzing things in a short period of time.
This is a trickier challenge, so someone who is really smart and notices the small details can do well. When the clock starts ticking, you’ll get even more excited as you race against time. Being good at this can provide you with valuable skills that can help you in many areas of life. Not only does it make you a better problem solver; It also makes your mind more flexible, which can help you in school, work, and your personal life.
See more : Brain Teaser: What is the Next Number 1, 3, 7, 12, 18, 26, 35, 45, 56,?
Although the puzzle is difficult, your goal is to find a solution that follows the rules and solve the puzzle. In the next section, you’ll learn more about how this math puzzle works and the satisfying answer that awaits you.
What values do A, B, and C represent in the equation AA + BB + CC = ABC?solution
This math puzzle is really hard and we hope you give it a try to find the answer.

A, B, and C are all different positive numbers. Let’s start with the value of A. When we add three two-digit numbers, the largest sum we can get is around 200. So A can be at most 2. But if A is a three-digit number, it must be at least 1 to be positive. So A is either 1 or 2.
Now, let’s look at the value of B. In the unit column, we have A + B + C equal to the result ending in C. This only happens if A and B add up to a number with a single digit of 0, meaning A + B equals 10. So if A is 1, then B is 9, and if A is 2, then B is 8. We have two cases to consider: 11 + 99 or 22 + 88.
See more : Observation Brain Test: If you have 50/50 Vision Find the Number 4867 among 4897 in 15 Secs
Let’s focus on the first case, 22 + 88. This gives us 110, and when we add C, we need the result to be 280 C. Since 110 has a zero in the ones digit, anything we add to it will give us the same ones digit, C. So we look at the tens place and we have 1 + C equals eight. Solving this equation, we find that C is equal to seven. But when we try 110 + 77, it doesn’t give the result we want (287). So this case doesn’t work.
Now, let’s consider the second possibility, 22 + 88. This gives us 110, and when we add C, we want the result to be 190. Again, unit position doesn’t help since 0 + C is always C. So we focus on the tens digit, where 1 + C equals 9. This means C is 8. We try 110 + 88 and the result is 198, which is the result we want (287). So the answer is 11 + 99 + 88 which equals 198.
Explore the hand-picked selection of mind-boggling brain teasers and math puzzles on NEWSTARS Education to take your mind game to new heights. Our diverse product range caters for every level of expertise.
trend
Determine the result of 144 ÷ 12 + 6 x 2 – 18 ÷ 3?
Apply the order of operations as usual. Division and multiplication proceed from left to right: 144 ÷ 12 equals 12, and 18 ÷ 3 equals 6. The equation now becomes 12 + 6 x 2 – 6. Next, perform multiplication, addition and subtraction from left to right: 6 x 2 equals 12, and 12 + 12 equals 24. Therefore, the solution is 24.
Solve the equation 72 ÷ 8 + 5 x 3 – 9 ÷ 3=?
Remember that you should perform division and multiplication from left to right. First, divide: 72 ÷ 8 equals 9, and 9 ÷ 3 equals 3. The equation now becomes 9 + 5 x 3 – 3. Next, multiply, add and subtract from left to right: 5 x 3 equals 15 and 9 + 15 equals 24. Therefore, the solution is 24.
Disclaimer: The above information is for general information purposes only. All information on this website is provided in good faith, but we make no representations or warranties, express or implied, as to the accuracy, adequacy, validity, reliability, availability or completeness of any information on this website.
Source: https://truongnguyenbinhkhiem.edu.vn
Category: Brain Teaser